Che cos'è il rendimento composto in modo continuo?

Il rendimento composto continuamente è ciò che accade quando l'interesse guadagnato su un investimento viene calcolato e reinvestito nel conto per un numero infinito di periodi. L'interesse viene calcolato sull'importo del capitale e sugli interessi accumulati nei periodi indicati e reinvestiti nel saldo di cassa.

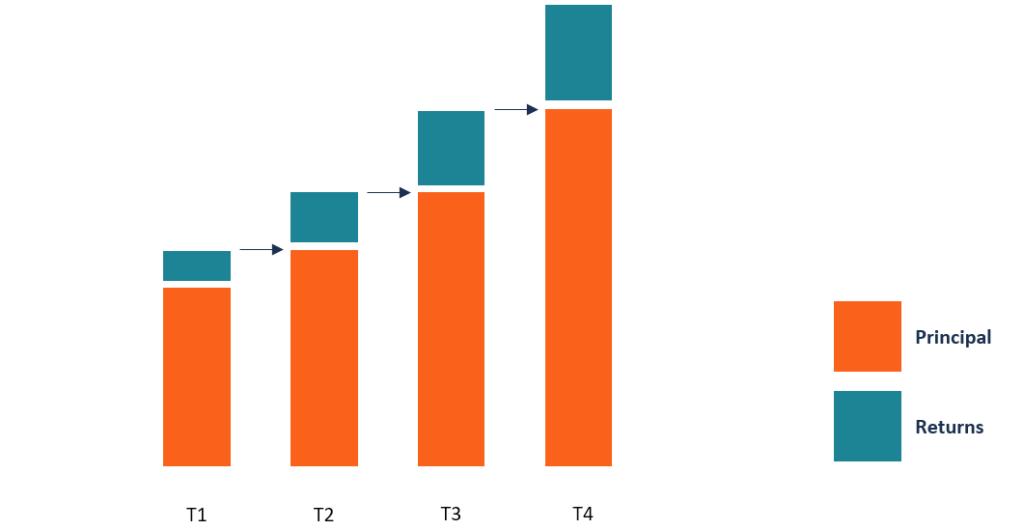
La capitalizzazione regolare viene calcolata su intervalli di tempo specifici come mensile, trimestrale, semestrale e su base annuale. La capitalizzazione continua è un caso estremo di questo tipo di capitalizzazione poiché calcola gli interessi su un numero infinito di periodi, piuttosto che assumere un numero specifico di periodi. La differenza tra gli interessi maturati con il metodo della capitalizzazione tradizionale e il metodo della capitalizzazione continua può essere significativa.

Rendimento composto annuale vs. rendimento composto continuamente

Gli investitori calcolano l'interesse o il tasso di rendimento Tasso di rendimento Il tasso di rendimento (ROR) è il guadagno o la perdita di un investimento in un periodo di tempo rapportato al costo iniziale dell'investimento espresso in percentuale. Questa guida insegna le formule più comuni sui loro investimenti utilizzando due tecniche principali:capitalizzazione annuale e capitalizzazione continua.

Composto annuale

La capitalizzazione annuale significa che il rendimento di un investimento viene calcolato ogni anno, ed è diverso dal semplice interesse. Il metodo di capitalizzazione annuale utilizza la seguente formula:

Totale =[Capitale x (1 + Interesse)] ^Numero di anni

Il rendimento dell'investimento si ottiene deducendo l'importo del capitale dai rendimenti totali ottenuti utilizzando la formula sopra.

Supponiamo che la società ABC abbia investito $ 10, 000 per acquistare uno strumento finanziario, e il tasso di rendimento è del 5% per due anni. Perciò, gli interessi maturati dall'investimento di ABC per il biennio sono i seguenti:

=[10, 000 x (1+0,05)^2

=(10, 000 x 1.1025)

=11, 025 – 10, 000

= $ 1, 025

Perciò, La società ABC ha guadagnato un interesse di $ 1, 025 sul suo investimento di $ 10, 000 in due anni.

Rendimento composto continuamente

A differenza della composizione annuale, che coinvolge un determinato numero di periodi, il numero di periodi utilizzati per la capitalizzazione continua è infinitamente numeroso. Invece di usare il numero di anni nell'equazione, la composizione continua utilizza una costante esponenziale per rappresentare il numero infinito di periodi. La formula per il capitale più gli interessi è la seguente:

Totale =Capitale x e^(Interessi x Anni)

In cui si:

• e – la funzione esponenziale, che è uguale a 2,71828.

Utilizzando l'esempio di Company ABC sopra, il ritorno sull'investimento può essere calcolato come segue quando si utilizza la capitalizzazione continua:

=10, 000 x 2,71828^(0,05 x 2)

=10, 000 x 1.1052

= $ 11, 052

Interesse =$ 11, 052 – $ 10, 000

= $ 1, 052

La differenza tra il ritorno sull'investimentoReturn on Investment (ROI)Return on Investment (ROI) è una misura di performance utilizzata per valutare i rendimenti di un investimento o confrontare l'efficienza di diversi investimenti. quando si utilizza la composizione continua rispetto alla composizione annuale è $ 27 ($ 1, 052 – $ 1025).

Quotidiano, Mensile, Trimestrale, e Semestrale Compounding

Oltre ai metodi di capitalizzazione annuale e continua, gli interessi possono anche essere capitalizzati a diversi intervalli di tempo, ad esempio giornalmente, mensile, trimestrale e semestrale.

Per illustrare la capitalizzazione a diversi intervalli di tempo, prendiamo un investimento iniziale di $ 1, 000 che paga un tasso di interesseTasso di interesseUn tasso di interesse si riferisce all'importo addebitato da un prestatore a un mutuatario per qualsiasi forma di debito dato, generalmente espresso in percentuale del capitale. dell'8%.

Composto giornaliero

La formula per la composizione giornaliera è la seguente:

=Capitale x (1+Interessi/365)^365

=1, 000 x (1 + 0,08/365) ^ 365

=1, 000 x (1 + 0,00022)^365

=1, 000 x (1.00022) ^ 365

=1, 000 x 1.0836

= $ 1, 083.60

Composizione mensile

La formula per gli intervalli mensili è la seguente:

=Capitale x (1+Interessi/12)^12

=1, 000 x (1+0,08/12) ^12

=1, 000 x [1+0,0067)^12

=1, 000 x (1.0067)^12

=1, 000 x (1.083)

= $ 1, 083.00

Composto trimestrale

La formula per la capitalizzazione trimestrale è la seguente:

=Capitale x (1 + interesse/4)^4

=1, 000 x (1 +0,08/4)^4

=1, 000 x (1 + 0,02)^4

=1, 000 x (1,02)^4

=1, 000 x 1.0824

= $ 1, 082.40

Composto semestrale

La formula per la capitalizzazione semestrale è la seguente:

=Capitale x (1 + interesse/2)^2

=1, 000 x (1 + 0,08/2)^2

=1, 000 x (1 + 0,04)^2

=1, 000 x (1,04)^2

=1, 000 x 1.0816

= $ 1, 081.60

Conclusione sugli intervalli composti

Dai calcoli di cui sopra, possiamo concludere che tutti gli intervalli producono un interesse quasi uguale, ma con una piccola variazione. Per esempio, la capitalizzazione trimestrale produce un interesse di $ 82,40, che è leggermente superiore all'interesse prodotto dalla capitalizzazione semestrale a 81,60 dollari.

Anche, il tasso mensile produce un interesse di $ 83, che è leggermente superiore all'interesse prodotto dai tassi trimestrali a 82,40 dollari. La capitalizzazione giornaliera produce un interesse più elevato di $ 83,60, che è leggermente superiore all'interesse a tassi mensili di $ 82,60.

Dal modello sopra, possiamo anche dire che piccoli intervalli di capitalizzazione degli interessi producono tassi di interesse più elevati rispetto a grandi intervalli di capitalizzazione.

Importanza del compounding continuo

La capitalizzazione continua offre vari vantaggi rispetto all'interesse sempliceInteresse sempliceFormula dell'interesse semplice, definizione ed esempio. L'interesse semplice è un calcolo dell'interesse che non tiene conto dell'effetto della capitalizzazione. In molti casi, composti di interesse con ogni periodo designato di un prestito, ma nel caso di semplice interesse, non è così. Il calcolo dell'interesse semplice è uguale all'importo del capitale moltiplicato per il tasso di interesse, moltiplicato per il numero di periodi. e composizione regolare. I vantaggi includono:

1. Reinvestire i guadagni perennemente

Uno dei vantaggi della capitalizzazione continua è che l'interesse viene reinvestito nel conto per un numero infinito di periodi. Significa che gli investitori godono della continua crescita dei loro portafogli, rispetto a quando guadagnano gli interessi mensilmente, trimestrale, o annualmente con capitalizzazione regolare.

2. L'importo degli interessi continuerà a crescere

Nella composizione continua, sia l'interesse che il capitale continuano a crescere, che rende più facile moltiplicare i rendimenti a lungo termine. Altre forme di capitalizzazione guadagnano solo interessi sul capitale e tale interesse viene pagato man mano che viene guadagnato. Reinvestire l'interesse consente all'investitore di guadagnare ad un tasso esponenziale per un numero infinito di periodi.

Risorse addizionali

Grazie per aver letto la spiegazione di CFI sul rendimento continuamente composto. CFI offre il Financial Modeling &Valuation Analyst (FMVA)™Diventa un Certified Financial Modeling &Valuation Analyst (FMVA)®La certificazione Financial Modeling and Valuation Analyst (FMVA)® di CFI ti aiuterà ad acquisire la fiducia di cui hai bisogno nella tua carriera finanziaria. Iscriviti oggi! programma di certificazione per coloro che desiderano portare la propria carriera a un livello superiore. Per continuare a imparare e ad avanzare nella tua carriera, le seguenti risorse CFI saranno utili:

• Tasso Annuo Percentuale (APR)Tasso Annuo Percentuale (APR)Il Tasso Annuo Percentuale (APR) è il tasso di interesse annuo che un individuo deve pagare su un prestito, o che ricevono su un conto deposito. In definitiva, APR è un semplice termine percentuale utilizzato per esprimere l'importo numerico pagato da un individuo o entità ogni anno per il privilegio di prendere in prestito denaro.
• Tasso di crescita annuale composto (CAGR) CAGRCAGR sta per tasso di crescita annuale composto. È una misura del tasso di crescita annuale di un investimento nel tempo, tenendo conto della composizione.
• Calcolatore del tasso di interesseCalcolatore del tasso di interesseCalcolatore del tasso di interesse per aiutarti a calcolare il tasso di interesse effettivo in base al numero di periodi, tipo di tasso di interesse, e l'importo del saldo iniziale.
• Principal PaymentPrincipal PaymentUn pagamento principale è un pagamento verso l'importo originale di un prestito che è dovuto. In altre parole, un pagamento principale è un pagamento effettuato su un prestito che riduce l'importo residuo del prestito dovuto, piuttosto che applicarsi al pagamento degli interessi addebitati sul prestito.