Che cos'è la durata modificata?

Durata modificata, una formula comunemente usata nelle valutazioni obbligazionarie, esprime la variazione del valore di un titolo a causa di una variazione dei tassi di interesseTasso di interesse variabilePer tasso di interesse variabile si intende un tasso di interesse variabile che varia lungo la durata dell'obbligazione di debito. È l'opposto di un tasso fisso. In altre parole, illustra l'effetto di una variazione di 100 punti base (1%) dei tassi di interesse sul prezzo di un'obbligazione.

La durata modificata illustra il concetto che i prezzi delle obbligazioni e i tassi di interesse si muovono in direzioni opposte:tassi di interesse più alti prezzi delle obbligazioni più bassi, e tassi di interesse più bassi aumentano i prezzi delle obbligazioni.

Formula per la durata modificata

La formula per la durata modificata è la seguente:

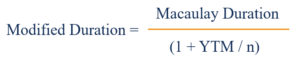
In cui si:

• Durata Macaulay è il numero medio ponderato di anni in cui un investitore deve mantenere la sua posizione nell'obbligazione in cui il valore attuale (PV) del flusso di cassa dell'obbligazione è uguale all'importo pagato per l'obbligazione. In altre parole, è il tempo che impiegherebbe un investitore a recuperare il denaro inizialmente investito nell'obbligazione
• YTM sta per Yield to Maturity Yield to Maturity (YTM) Yield to Maturity (YTM) - altrimenti indicato come rimborso o rendimento contabile - è il tasso di rendimento speculativo o il tasso di interesse di un titolo a tasso fisso. ed è il rendimento totale di un'obbligazione se detenuta fino alla scadenza
• n è il numero di periodi di cedola all'anno.

Comprendere la durata di Macaulay

Per arrivare alla durata modificata di un'obbligazione, è importante comprendere la componente del numeratore – la durata di Macaulay – nella formula di durata modificata.

La durata di Macaulay è la media ponderata del tempo fino alla ricezione dei flussi di cassa di un'obbligazione. In parole povere, le misure di durata di Macaulay, in anni, la quantità di tempo necessaria a un investitore per rimborsare il suo investimento iniziale in un'obbligazione. Un'obbligazione con una duration Macaulay più alta sarà più sensibile alle variazioni dei tassi di interesse.

La formula per la durata di Macaulay è la seguente:

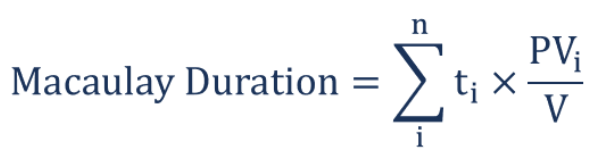
In cui si:

• T _io è il periodo di tempo
• PV _io è il valore attuale del flusso di cassa ponderato nel tempo
• V è il valore attuale di tutti i flussi di cassa.

Di seguito è riportato un esempio di calcolo della durata Macaulay su un'obbligazione.

Esempio di durata di Macaulay

Tim detiene un'obbligazione a 5 anni con un valore nominale di $ 1, 000 e un tasso di cedola annualeTasso di cedolaUn tasso di cedola è l'importo del reddito da interessi annuo pagato a un detentore di obbligazioni, in base al valore nominale dell'obbligazione. del 5%. Il tasso di interesse attuale è del 7%, e Tim vorrebbe determinare la durata Macaulay dell'obbligazione. Il calcolo è riportato di seguito:

La durata Macaulay per l'obbligazione a 5 anni è calcolata come $ 4152,27 / $ 918,00 = 4,52 anni .

Mettere insieme

Ora che abbiamo capito e sappiamo come calcolare la durata di Macaulay, possiamo determinare la durata modificata.

Utilizzando l'esempio sopra, inseriamo semplicemente le cifre nella formula per determinare la durata modificata:

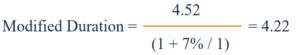
La durata modificata è 4.22 .

Interpretazione della durata modificata

Come interpretiamo il risultato sopra? Ricordiamo che la duration modificata illustra l'effetto di una variazione di 100 punti base (1%) dei tassi di interesse sul prezzo di un'obbligazione.

Perciò,

• Se i tassi di interesse aumento dell'1%, il prezzo del titolo a 5 anni sarà diminuire del 4,22%.
• Se i tassi di interesse diminuire dell'1%, il prezzo del titolo a 5 anni sarà aumento del 4,22%.

La duration modificata fornisce una buona misurazione della sensibilità di un'obbligazione alle variazioni dei tassi di interesse. Maggiore è la durata Macaulay di un'obbligazione, maggiore è la durata modificata risultante e la volatilità alle variazioni dei tassi di interesse.

Risorse addizionali

CFI è il fornitore ufficiale della Global Financial Modeling &Valuation Analyst (FMVA)™Diventa un Certified Financial Modeling &Valuation Analyst (FMVA)®La certificazione Financial Modeling and Valuation Analyst (FMVA)® di CFI ti aiuterà ad acquisire la fiducia di cui hai bisogno nel tuo carriera finanziaria. Iscriviti oggi! programma di certificazione, progettato per aiutare chiunque a diventare un analista finanziario di livello mondiale. Per continuare ad avanzare nella tua carriera, le risorse aggiuntive di seguito saranno utili:

• Prezzo delle obbligazioniPrezzo delle obbligazioniIl prezzo delle obbligazioni è la scienza del calcolo del prezzo di emissione di un'obbligazione in base alla cedola, valore nominale, rendimento e termine alla scadenza. Il prezzo delle obbligazioni consente agli investitori
• Durata effettiva Durata effettiva La durata effettiva è la sensibilità del prezzo di un'obbligazione rispetto alla curva dei rendimenti di riferimento. Un modo per valutare il rischio di un'obbligazione è stimare il
• Funzione DURATA in Excel Funzione DURATA La funzione DURATA è classificata in Funzioni finanziarie di Excel. Aiuta a calcolare la durata di Macauley. La funzione calcola la durata di un titolo che paga interessi su base periodica con un valore nominale di $ 100.
• Azionario vs Reddito Fisso Azionario vs Reddito Fisso Azionario vs Reddito Fisso. I prodotti azionari e obbligazionari sono strumenti finanziari che presentano differenze molto importanti che ogni analista finanziario dovrebbe conoscere. Gli investimenti azionari sono generalmente costituiti da azioni o fondi azionari, mentre i titoli a reddito fisso sono generalmente costituiti da obbligazioni societarie o governative.