Non tutte le grandi mosse sono uguali:volatilità e probabilità
Guarda le notizie finanziarie abbastanza a lungo, e sei destinato a sentire qualcuno incanalare Johnny Most a una partita dei Celtics:"XYZ ha guadagnato 5 punti!" "ABCD è sceso del 3%!" Le schiacciate a sorpresa e le variazioni del prezzo delle azioni spesso significano grandi storie. E le notizie di mercato potrebbero essere piuttosto noiose senza il dramma. Ma se non metti la volatilità ("vol") nel contesto, è difficile dire se tutta l'eccitazione per un titolo sia causata da una tripla vincente, o un semplice tiro libero del primo quarto.
Crea un piano di gioco
È qui che entri tu, il commerciante esperto, che possono interpretare e inquadrare determinati eventi di mercato facendo affidamento su un mix di vol e statistiche. Niente di troppo complesso, ma abbastanza per rispondere alla domanda, quanto è grande?
Questo è importante perché può aiutarti a incorporare le notizie di mercato in una strategia di trading. Sei un trader di slancio che cerca di acquistare forza o corto di debolezza? Un contrarian che cerca di acquistare azioni con grandi svendite, o short stock dopo grandi rally? Qualunque sia la tua strategia, è fondamentale disporre di una metrica che ti aiuti a determinare se un grande cambiamento di prezzo merita la tua attenzione. Iniziamo.
Primo, alcune statistiche. In alcuni modelli e teorie finanziarie (ad es. Black-Scholes), si presume che le variazioni percentuali dei prezzi delle azioni e dell'indice siano distribuite normalmente. Pensa a una curva a campana con un picco nel mezzo che rappresenta teoricamente una variazione dello 0%. Troverai grandi movimenti verso il basso sul lato sinistro, e big up si muove sul lato destro. In realtà, le variazioni di prezzo in tutti i casi possono o non possono essere normalmente distribuite, ma la distribuzione normale ci consente di determinare un paio di cose utili su quanto grande è "grande".
Una deviazione standard su e giù dalla media copre teoricamente circa il 68% delle variazioni di prezzo. Due deviazioni standard su e giù coprono circa il 95%. E tre deviazioni standard su e giù coprono circa il 99%. Ulteriore, il vol di un titolo o di un indice determina la dimensione di una deviazione standard in termini di prezzo. Più alto è il vol, maggiore è la variazione in dollari del prezzo delle azioni rappresentata dalla deviazione standard. Sì, una deviazione standard copre il 68% di una variazione di prezzo teorica. Ma vol determina se tali variazioni di prezzo sono $ 1 o $ 10. Una variazione di $ 1 in un'azione da $ 10 è una percentuale molto più grande (10%) di una variazione di $ 1 in un'azione da $ 500 (0,2%). E se le azioni da $ 10 potrebbero cambiare quel 10%, o che $ 500 azioni potrebbero cambiare quello 0,2%, dipende dalla volatilità di ciascun titolo.
Considera un campo di gioco equo
Un'azione da $ 10 con una volatilità del 15% avrebbe un intervallo teorico compreso tra $ 8,50 e $ 11,50 il 68% delle volte in un anno. Per ottenerlo, moltiplicare il prezzo delle azioni ($10) per la volatilità (15%), quindi aggiungi o sottrai quello dal prezzo delle azioni prevalente. Moltiplicando il prezzo delle azioni per il suo volume si ottiene una deviazione standard teorica per un anno.
Ora, diciamo che vuoi conoscere la deviazione standard per un giorno, settimana, o mese. Nessun problema. Basta moltiplicare quel numero di volume (sempre un numero di un anno sulla piattaforma thinkorswim® di TD Ameritrade) per la radice quadrata del periodo di tempo per adattarlo all'intervallo di tempo desiderato. Per esempio, per la deviazione standard di un giorno di negoziazione, dividere uno per il numero di giorni di negoziazione in un anno (qui si usa 262), prendi la radice quadrata, moltiplicare per il vol, quindi moltiplicalo per il prezzo delle azioni.
Per quel titolo da $ 10 con un 15% vol, la deviazione standard di un giorno sarebbe la radice quadrata di 1/262 (o 0,0618) x 0,15 x $ 10 =$ 0,093. Teoricamente, quel titolo potrebbe atterrare in un intervallo compreso tra $ 9,907 e $ 10,093, Il 68% delle volte. Se il titolo è sceso di $ 0,19 in un giorno da $ 10 a $ 9,81, sarebbe teoricamente sceso di poco più di due deviazioni standard basate su quella volatilità del 15%. Due deviazioni standard sono una mossa piuttosto grande secondo la distribuzione normale, anche se il prezzo cambia solo $ 0,19.
Esegui le tue riproduzioni
Mettiamo tutto in pratica. Supponiamo che un'azione sia aumentata da $ 80 di lunedì a $ 85 di martedì. Di lunedi, lo stock ha avuto un vol complessivo del 30%. Così, 0,0618 x 0,30 x $ 80 =$ 1,48. E $ 1,48 è una deviazione standard basata sul prezzo e sulla volatilità di lunedì. Teoricamente, il 68% delle volte, il titolo potrebbe aver chiuso in un intervallo tra $ 78,52 (in calo di $ 1,48) e $ 81,48 (in aumento di $ 1,48) martedì. Ma invece, è aumentato di $ 5 martedì. Dividi la variazione di $ 5 nel prezzo delle azioni per la deviazione standard teorica di $ 1,48 per vedere quante deviazioni standard ha registrato un rally ($ 5 / $ 1,48 =3,38 deviazioni standard). Teoricamente, con il 99% dei potenziali prezzi delle azioni in aumento o in diminuzione di tre deviazioni standard, una variazione di prezzo della deviazione standard di 3,38 è piuttosto insolita.
Se il vol di quel titolo da $ 80 era del 60% lunedì, quindi 0,0618 x 0,60 x $ 80 =$ 2,97. Questa è teoricamente una deviazione standard, e $5/2,97$ =1,68. Una variazione di prezzo di deviazione standard di 1,68 è grande, ma non insolito, teoricamente.
La variazione di prezzo di $ 5 per le azioni da $ 80 è lo stesso p/l per 100 azioni. Ma in termini statistici, significa cose diverse. Il cambio di $ 5 quando il volume era del 30% è degno di un po' di eccitazione. La variazione di $ 5 quando il volume era del 60%, Non così tanto. In altre parole, quando il volume era del 60%, il mercato forse si aspettava un grande cambiamento di prezzo, e la mossa di $ 5 non era così grande come avrebbe potuto essere.
Per ottenere i numeri di vol e prezzo delle azioni per eseguire questa analisi, colpire il Grafici pagina di thinkorswim (Figura 1).
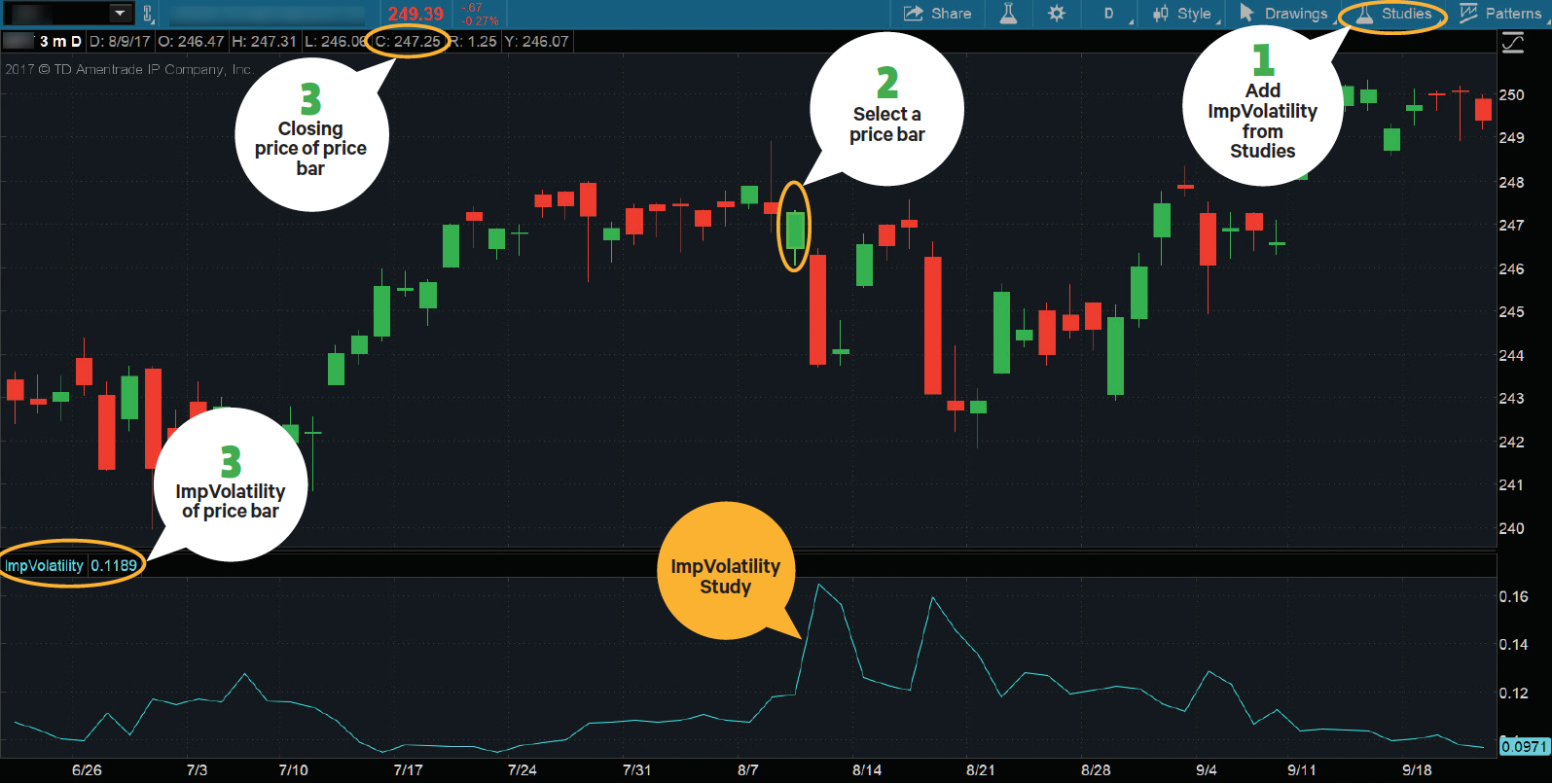
FIGURA 1:DIMENSIONAMENTO DELLA DEVIAZIONE STANDARD DELLA VARIAZIONE DI PREZZO.
Passa il cursore su una barra del prezzo prima e dopo la variazione di prezzo in questione. Prossimo, ottenere il prezzo di chiusura e il vol implicito complessivo dell'azione o dell'indice sottostante. Quindi inserisci i numeri nella formula e calcola la deviazione standard della variazione di prezzo. Fonte:thinkorswim® di TD Ameritrade. Solo a scopo illustrativo.
1—Da “Studi, ” aggiungere lo studio “ImpVolatilty” ai Grafici, che mostra il volume implicito complessivo delle opzioni su azioni.
2—Imposta il cursore su una data precedente alla variazione di prezzo in questione.
3—Vedrai ora il prezzo di chiusura dell'azione o dell'indice sottostante in alto a sinistra del grafico, e il volume complessivo implicito del titolo o dell'indice nell'angolo in alto a sinistra della finestra di studio ImpVolatility.
Quindi considera il prezzo dell'azione o dell'indice dopo un grande cambiamento, e sottrarre il prezzo di chiusura della data precedente da quel prezzo post-movimento per ottenere la variazione di prezzo.
Regola il volume per tempo, fare qualche moltiplicazione e divisione, e determinare le deviazioni standard della variazione di prezzo.
Gioco corretto
Perché devi regolare vol per la radice quadrata dell'intervallo di tempo? Se un titolo sale di +1% un giorno, e giù -0,999% il prossimo, il prezzo delle azioni ha avuto una variazione netta quasi nulla. Ma era volatile? Sì. Per assicurarsi che le variazioni di prezzo positive non compensino le variazioni di prezzo negative (il che darebbe l'impressione che non ci siano volumi), tutte le variazioni di prezzo sono quadrate per renderle positive. Facendo la media delle variazioni al quadrato, ottieni una varianza direttamente correlata al tempo. Perché è un quadrato dei rendimenti azionari, quella varianza è più difficile da interpretare. Così, prendiamo la sua radice quadrata per tornare al volume dei rendimenti azionari. Se prendi la radice quadrata della varianza, devi prendere la radice quadrata del tempo, pure. Ecco perché vol è correlato alla radice quadrata del tempo.
Ora, le prestazioni passate non garantiscono le prestazioni future, e vol non è un perfetto predittore di potenziali rendimenti futuri. A volte può sottovalutare le potenziali variazioni di prezzo di un titolo, mentre altre volte può sopravvalutare. In altre parole, vol potrebbe prevedere il movimento del 3% di un titolo in un mese, quando effettivamente si è mosso del 5% (sottostimando). Oppure vol potrebbe prevedere il movimento del 10% di un'azione in un mese quando in realtà si è mosso dell'8% (sovrastimando). Tieni inoltre presente che la normale distribuzione alla base non è un perfetto descrittore di rendimenti. In pratica, i rendimenti sono raramente distribuiti lungo una distribuzione normale "pulita".
Tutto sommato, questa analisi fornisce un contesto al movimento dei prezzi. Tornando alle azioni da 80 dollari, se l'aumento di prezzo di $ 5 rappresentasse una variazione della deviazione standard di 3,38 statisticamente meno probabile, un trader ribassista contrarian potrebbe cogliere questa potenziale opportunità per entrare in un'operazione, mentre un trader rialzista potrebbe aspettare che il titolo scenda prima di entrare. Se l'aumento del prezzo di $ 5 rappresentava una variazione della deviazione standard di 1,68 statisticamente più probabile, l'orso contrarian potrebbe aspettare che il titolo si rialzi prima di venderlo allo scoperto, mentre un momentum rialzista potrebbe diventare lungo a quel punto e vedere un potenziale di rialzo maggiore.
Nessun tiro libero
Usa vol e le statistiche come un'ulteriore metrica nella tua casella degli strumenti di trading. Non è una strategia in sé e per sé. Ma può aiutarti a determinare i punti di entrata e di uscita per determinate operazioni quantificando la "grandezza" delle variazioni di prezzo.
Opzione
-
 Paga con un selfie:quanto sono sicuri i nuovi modi di pagare?
Paga con un selfie:quanto sono sicuri i nuovi modi di pagare? Nel 2016, più della metà di tutti gli acquisti negli Stati Uniti sono stati effettuati online anziché in un negozio fisico. Dai selfie-pagamenti ai bot di Facebook Messenger, ora cè una lunga lista di...
-
 Perché la migliore strategia di ricompensa con carta di credito è lenta
Perché la migliore strategia di ricompensa con carta di credito è lenta Per coloro che si precipitano nel gioco dei premi con carta di credito, le conseguenze possono essere gravi e durature. Dopotutto, il debito medio della carta di credito per famiglia indebitata era di...
-
 Devo vendere la mia polizza di assicurazione sulla vita?
Devo vendere la mia polizza di assicurazione sulla vita? Come qualcuno che ha costantemente investito i suoi sudati soldi in premi di assicurazione sulla vita, quando il tempo arriva, chiedendoti:devo vendere la mia polizza di assicurazione sulla vita? È cr...
-
 Qual è il prezzo indicato?
Qual è il prezzo indicato? Il prezzo quotato è il più recente – o ultimo – prezzo al quale unattività finanziaria Attività finanziarie Le attività finanziarie si riferiscono ad attività che derivano da accordi contrattuali sui ...