Definizione di relazione lineare

Che cos'è una relazione lineare?

Una relazione lineare (o associazione lineare) è un termine statistico utilizzato per descrivere una relazione lineare tra due variabili. Le relazioni lineari possono essere espresse sia in formato grafico in cui la variabile e la costante sono collegate tramite una linea retta, sia in formato matematico in cui la variabile indipendente è moltiplicata per il coefficiente di pendenza, aggiunto da una costante, che determina la variabile dipendente.

Una relazione lineare può essere contrapposta a una relazione polinomiale o non lineare (curva).

Punti chiave

• Una relazione lineare (o associazione lineare) è un termine statistico utilizzato per descrivere una relazione lineare tra due variabili.
• Le relazioni lineari possono essere espresse in formato grafico o come equazione matematica della forma y =mx + b.
• Le relazioni lineari sono abbastanza comuni nella vita quotidiana.

L'equazione lineare è:

Matematicamente, una relazione lineare è quella che soddisfa l'equazione:

sì = m X + B dove: m = pendenza B = y-intercetta \begin{allineato} &y =mx + b \\ &\textbf{dove:}\\ &m=\text{pendenza}\\ &b=\text{intercetta y}\\ \end{allineato} ​y=mx+bdove:m=pendenzab=y-intercetta​

In questa equazione, “x” e “y” sono due variabili legate dai parametri “m” e “b”. Graficamente, y =mx + b traccia nel piano x-y come una linea con pendenza "m" e y-intercetta "b". L'intercetta y "b" è semplicemente il valore di "y" quando x=0. La pendenza "m" viene calcolata da due punti singoli qualsiasi (x ₁ , sì ₁ ) e (x ₂ , sì ₂ ) come:

m = ( sì 2 − sì 1 ) ( X 2 − X 1 ) m =\frac{(y_2 - y_1)}{(x_2 - x_1)} m=(x2​−x1​)(y2​−y1​)​

Relazione lineare

Cosa ti dice una relazione lineare?

Ci sono tre serie di criteri necessari che un'equazione deve soddisfare per qualificarsi come lineare:un'equazione che esprime una relazione lineare non può consistere di più di due variabili, tutte le variabili in un'equazione devono essere alla prima potenza, e l'equazione deve essere rappresentata come una linea retta.

Una relazione lineare comunemente usata è una correlazione, che descrive quanto vicino alla moda lineare una variabile cambia in relazione ai cambiamenti in un'altra variabile.

In econometria, la regressione lineare è un metodo spesso utilizzato per generare relazioni lineari per spiegare vari fenomeni. È comunemente usato per estrapolare eventi dal passato per fare previsioni per il futuro. Non tutte le relazioni sono lineari, però. Alcuni dati descrivono relazioni curve (come le relazioni polinomiali) mentre altri dati non possono essere parametrizzati.

Funzioni lineari

Matematicamente simile a una relazione lineare è il concetto di funzione lineare. In una variabile, una funzione lineare può essere scritta come segue:

F ( X ) = m X + B dove: m = pendenza B = y-intercetta \begin{allineato} &f(x) =mx + b \\ &\textbf{dove:}\\ &m=\text{pendenza}\\ &b=\text{intercetta y}\\ \end{allineato} ​f(x)=mx+bdove:m=pendenzab=y-intercetta​

Questo è identico alla formula data per una relazione lineare tranne che il simbolo f(x) è usato al posto di y. Questa sostituzione è fatta per evidenziare il significato che x è mappato su f(x), considerando che l'uso di sì indica semplicemente che x e y sono due quantità, riferito da A e B.

Nello studio dell'algebra lineare, le proprietà delle funzioni lineari sono ampiamente studiate e rese rigorose. Dato uno scalare C e due vettori A e B da R ⁿ , la definizione più generale di funzione lineare afferma che: C × F ( UN + B ) = C × F ( UN ) + C × F ( B ) c \times f(A + B) =c \times f(A) + c \times f(B) c×f(A+B)=c×f(A)+c×f(B)

Esempi di relazioni lineari

Esempio 1

Le relazioni lineari sono piuttosto comuni nella vita quotidiana. Prendiamo ad esempio il concetto di velocità. La formula che usiamo per calcolare la velocità è la seguente:la velocità è la distanza percorsa nel tempo. Se qualcuno in un minivan Chrysler Town and Country bianco del 2007 sta viaggiando tra Sacramento e Marysville in California, un tratto di 41,3 miglia sull'autostrada 99, e il viaggio completo finisce per impiegare 40 minuti, avrà viaggiato appena al di sotto dei 60 mph.

Sebbene ci siano più di due variabili in questa equazione, è ancora un'equazione lineare perché una delle variabili sarà sempre una costante (distanza).

Esempio 2

Una relazione lineare può essere trovata anche nell'equazione distanza =velocità x tempo. Poiché la distanza è un numero positivo (nella maggior parte dei casi), questa relazione lineare sarebbe espressa nel quadrante in alto a destra di un grafico con un asse X e Y.

Se una bicicletta fatta per due viaggiasse a una velocità di 30 miglia orarie per 20 ore, il pilota finirà per percorrere 600 miglia. Rappresentato graficamente con la distanza sull'asse Y e il tempo sull'asse X, una linea che traccia la distanza in quelle 20 ore viaggerebbe direttamente dalla convergenza degli assi X e Y.

Esempio 3

Per convertire Celsius in Fahrenheit, o Fahrenheit in Celsius, useresti le equazioni qui sotto. Queste equazioni esprimono una relazione lineare su un grafico:

° C = 5 9 ( ° F − 3 2 ) \grado C =\frac{5}{9}(\grado F - 32) °C=95​(°F−32)

° F = 9 5 ° C + 3 2 \grado F =\frac{9}{5}\grado C + 32 °F=59°C+32

Esempio 4

Supponiamo che la variabile indipendente sia la dimensione di una casa (misurata dalla metratura) che determina il prezzo di mercato di una casa (la variabile dipendente) quando viene moltiplicata per il coefficiente di pendenza di 207,65 e quindi aggiunta al termine costante $10 , 500. Se la metratura di una casa è 1, 250 allora il valore di mercato della casa è (1, 250 x 207.65) + $ 10, 500 =$ 270, 062.50. Graficamente, e matematicamente, appare come segue:

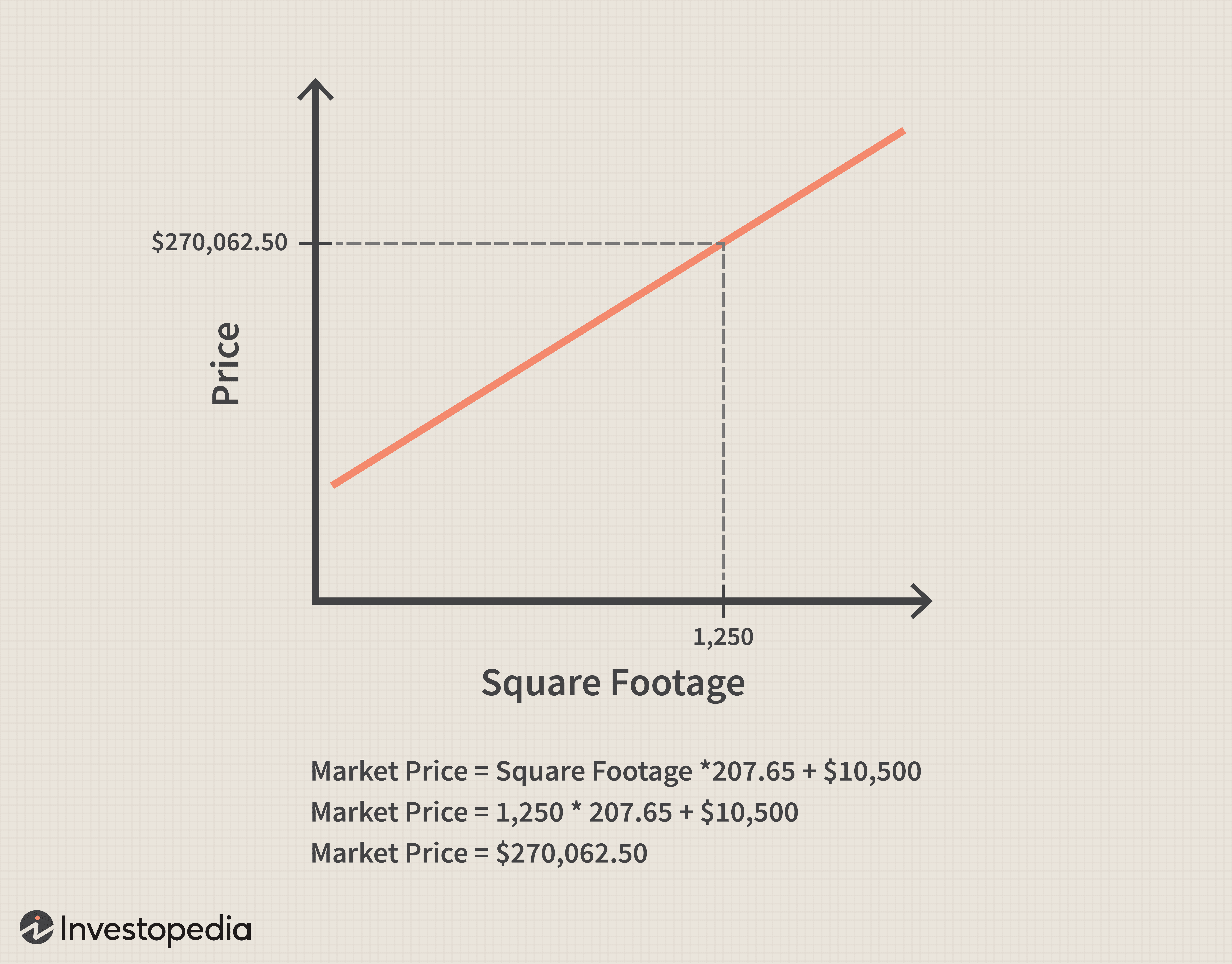
In questo esempio, all'aumentare delle dimensioni della casa, il valore di mercato della casa aumenta in modo lineare.

Alcune relazioni lineari tra due oggetti possono essere chiamate "relazioni proporzionali". Questa relazione appare come

sì = K × X dove: K = costante sì , X = quantità proporzionali \begin{allineato} &Y =k \times X \\ &\textbf{dove:}\\ &k=\text{costante}\\ &Y, X=\text{quantità proporzionali}\\ \end{allineato} ​Y=k×Xdove:k=costanteY, X=quantità proporzionali​

Quando si analizzano i dati comportamentali, raramente esiste una relazione lineare perfetta tra le variabili. Però, le linee di tendenza possono essere trovate nei dati che formano una versione approssimativa di una relazione lineare. Per esempio, potresti guardare le vendite giornaliere di gelato e l'alta temperatura giornaliera come le due variabili in gioco in un grafico e trovare una relazione lineare grezza tra le due.