Test di ipotesi in finanza:concetto ed esempi
Il tuo consulente per gli investimenti ti propone un piano di investimento a reddito mensile che promette un rendimento variabile ogni mese. Investirai in esso solo se ti viene assicurato un reddito mensile medio di $ 180. Il tuo consulente ti dice anche che negli ultimi 300 mesi, lo schema ha avuto ritorni di investimento con un valore medio di $ 190 e una deviazione standard di $ 75. Dovresti investire in questo schema? La verifica delle ipotesi viene in aiuto a tale processo decisionale.
Punti chiave
- Il test di ipotesi è uno strumento matematico per confermare un'affermazione o un'idea finanziaria o commerciale.
- Il test di ipotesi è utile per gli investitori che cercano di decidere in cosa investire e se è probabile che lo strumento fornisca un rendimento soddisfacente.
- Nonostante l'esistenza di diverse metodologie di verifica delle ipotesi, vengono utilizzati gli stessi quattro passaggi:definire l'ipotesi, fissare i criteri, calcolare la statistica, e giungere a una conclusione.
- Questo modello matematico, come la maggior parte degli strumenti e dei modelli statistici, ha dei limiti ed è soggetto a certi errori, richiedendo agli investitori di considerare anche altri modelli in combinazione con questo
Che cos'è il test di ipotesi?
Ipotesi o test di significatività è un modello matematico per testare un'affermazione, idea o ipotesi su un parametro di interesse in un dato insieme di popolazione, utilizzando i dati misurati in un set di campioni. I calcoli vengono eseguiti su campioni selezionati per raccogliere informazioni più decisive sulle caratteristiche dell'intera popolazione, che consente un modo sistematico per testare affermazioni o idee sull'intero set di dati.
Ecco un semplice esempio:un preside di una scuola riferisce che gli studenti della loro scuola ottengono una media di 7 su 10 negli esami. Per verificare questa “ipotesi, " Registriamo voti di diciamo 30 studenti (campione) dall'intera popolazione studentesca della scuola (diciamo 300) e calcoliamo la media di quel campione. Possiamo quindi confrontare la media campionaria (calcolata) con la media (riportata) della popolazione e tentare di confermare l'ipotesi.
Per fare un altro esempio, il rendimento annuo di un particolare fondo comune è dell'8%. Supponiamo che il fondo comune di investimento esista da 20 anni. Prendiamo un campione casuale di rendimenti annuali del fondo comune di investimento per, dire, cinque anni (campione) e calcolarne la media. Quindi confrontiamo la media campionaria (calcolata) con la media (presunta) della popolazione per verificare l'ipotesi.
Questo articolo presuppone la familiarità dei lettori con i concetti di una normale tabella di distribuzione, formula, p-value e relative basi di statistica.
Esistono diverse metodologie per la verifica delle ipotesi, ma sono coinvolti gli stessi quattro passaggi fondamentali:
Passaggio 1:definire l'ipotesi
Generalmente, il valore riportato (o la statistica del sinistro) è indicato come ipotesi e si presume che sia vero. Per gli esempi precedenti, l'ipotesi sarà:
- Esempio A:gli studenti della scuola ottengono una media di 7 su 10 negli esami.
- Esempio B:Il rendimento annuo del fondo comune è dell'8% annuo.
Questa descrizione dichiarata costituisce il “ Ipotesi nulla (H 0 ) " ed è presunto per essere vero - il modo in cui un imputato in un processo con giuria è presunto innocente fino a quando non viene dimostrato colpevole dalle prove presentate in tribunale. Allo stesso modo, il test di ipotesi inizia affermando e assumendo una "ipotesi nulla, ” e quindi il processo determina se è probabile che l'assunzione sia vera o falsa.
Il punto importante da notare è che stiamo testando l'ipotesi nulla perché c'è un elemento di dubbio sulla sua validità. Qualsiasi informazione contraria all'ipotesi nulla dichiarata viene catturata nel Ipotesi alternativa (H 1 ). Per gli esempi precedenti, l'ipotesi alternativa sarà:
- Gli studenti ottengono una media che è non uguale a 7.
- Il rendimento annuo del fondo comune è di non pari all'8% annuo.
In altre parole, l'ipotesi alternativa è una contraddizione diretta dell'ipotesi nulla.
Come in un processo, la giuria assume l'innocenza dell'imputato (ipotesi nulla). Il pubblico ministero deve dimostrare il contrario (ipotesi alternativa). Allo stesso modo, il ricercatore deve dimostrare che l'ipotesi nulla è vera o falsa. Se il pubblico ministero non prova l'ipotesi alternativa, la giuria deve lasciar partire l'imputato (basando la decisione sull'ipotesi nulla). Allo stesso modo, se il ricercatore non riesce a dimostrare un'ipotesi alternativa (o semplicemente non fa nulla), allora si assume che l'ipotesi nulla sia vera.
I criteri decisionali devono essere basati su determinati parametri di set di dati.
Passaggio 2:imposta i criteri
I criteri decisionali devono essere basati su determinati parametri di set di dati ed è qui che entra in scena il collegamento alla distribuzione normale.
Secondo il postulato statistico standard sulla distribuzione campionaria, “Per qualsiasi dimensione del campione n, la distribuzione campionaria di X̅ è normale se la popolazione X da cui è tratto il campione è distribuita normalmente. Quindi, le probabilità di tutte le altre possibili medie campionarie che si potrebbe selezionare sono normalmente distribuiti.
Per es. determinare se il rendimento medio giornaliero, di qualsiasi azione quotata sul mercato azionario XYZ, intorno a Capodanno è maggiore del 2%.
h 0 :Ipotesi nulla:media =2%
h 1 :Ipotesi alternativa:media> 2% (questo è ciò che vogliamo dimostrare)
Prendi il campione (diciamo di 50 titoli su un totale di 500) e calcola la media del campione.
Per una distribuzione normale, Il 95% dei valori rientra in due deviazioni standard della media della popolazione. Quindi, questa distribuzione normale e l'assunzione del limite centrale per il set di dati campione ci consente di stabilire il 5% come livello di significatività. Ha senso come, sotto questa ipotesi, c'è meno del 5% di probabilità (100-95) di ottenere valori anomali che sono oltre due deviazioni standard dalla media della popolazione. A seconda della natura dei set di dati, altri livelli di significatività possono essere assunti all'1%, 5% o 10%. Per i calcoli finanziari (inclusa la finanza comportamentale), 5% è il limite generalmente accettato. Se troviamo calcoli che vanno oltre le solite due deviazioni standard, allora abbiamo un caso forte di outlier per rifiutare l'ipotesi nulla.
Graficamente, è rappresentato come segue:
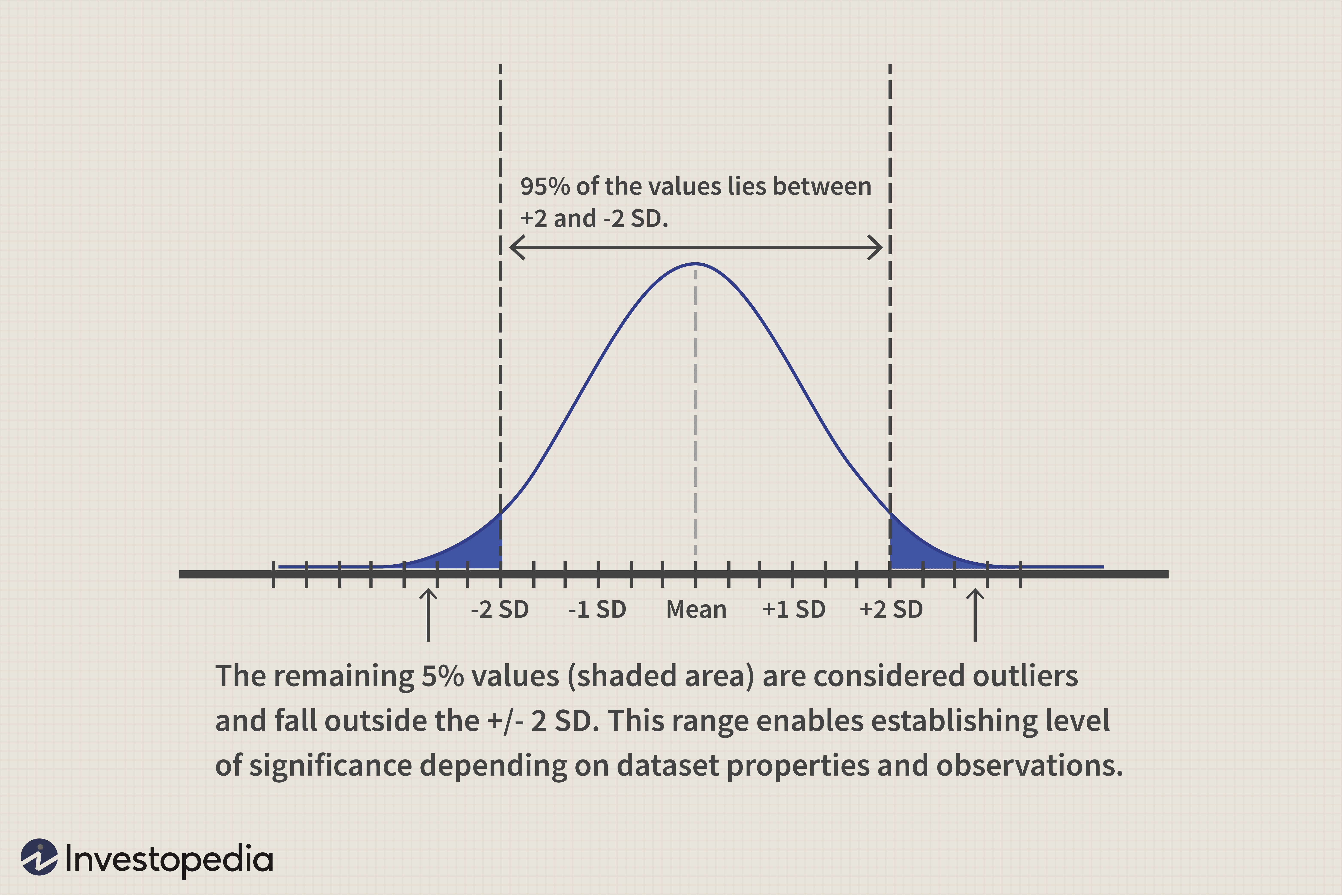
Nell'esempio sopra, se la media del campione è molto maggiore del 2% (diciamo 3,5%), allora rifiutiamo l'ipotesi nulla. L'ipotesi alternativa (media>2%) è accettata, il che conferma che il rendimento medio giornaliero dei titoli è infatti superiore al 2%.
Però, se è improbabile che la media del campione sia significativamente maggiore del 2% (e rimane a, dire, circa il 2,2% allora NON possiamo rifiutare l'ipotesi nulla. La sfida arriva su come decidere su casi così ravvicinati. Per trarre una conclusione da campioni e risultati selezionati, un livello di significatività deve essere determinato, che consente di trarre una conclusione sull'ipotesi nulla. L'ipotesi alternativa consente di stabilire il livello di significatività o il concetto di "valore critico" per decidere su tali casi a distanza ravvicinata.
Secondo la definizione standard del libro di testo, “Un valore critico è un valore di cutoff che definisce i confini oltre i quali è possibile ottenere meno del 5% della media campionaria se l'ipotesi nulla è vera. Le medie campione ottenute oltre un valore critico risulteranno nella decisione di rifiutare l'ipotesi nulla." Nell'esempio sopra, se abbiamo definito il valore critico come 2,1%, e la media calcolata arriva al 2,2%, allora rifiutiamo l'ipotesi nulla. Un valore critico stabilisce una chiara demarcazione tra accettazione o rifiuto.
Passaggio 3:calcola la statistica
Questo passaggio comporta il calcolo delle cifre richieste, note come statistiche di test (come media, punteggio z, valore p, eccetera.), per il campione selezionato. (Ci arriveremo in una sezione successiva.)
Passaggio 4:raggiungi una conclusione
Con i valori calcolati, decidere sull'ipotesi nulla. Se la probabilità di ottenere una media campionaria è inferiore al 5%, allora la conclusione è rifiutare l'ipotesi nulla. Altrimenti, accettare e mantenere l'ipotesi nulla.
Tipi di errori
Ci possono essere quattro possibili risultati nel processo decisionale basato su campioni, per quanto riguarda la corretta applicabilità all'intera popolazione:
Decisione di mantenere
Decisione di rifiutare
Si applica a tutta la popolazione
Corretta
Errato
(Errore di TIPO 1 - a)
Non si applica all'intera popolazione
Errato
(Errore di TIPO 2 - b)
Corretta
I casi “Corretti” sono quelli in cui le decisioni prese sui campioni sono realmente applicabili all'intera popolazione. I casi di errore sorgono quando si decide di conservare (o rifiutare) l'ipotesi nulla in base ai calcoli del campione, ma quella decisione non si applica realmente all'intera popolazione. Questi casi costituiscono errori di tipo 1 (alfa) e di tipo 2 (beta), come indicato nella tabella sopra.
La selezione del valore critico corretto consente di eliminare gli errori alfa di tipo 1 o di limitarli a un intervallo accettabile.
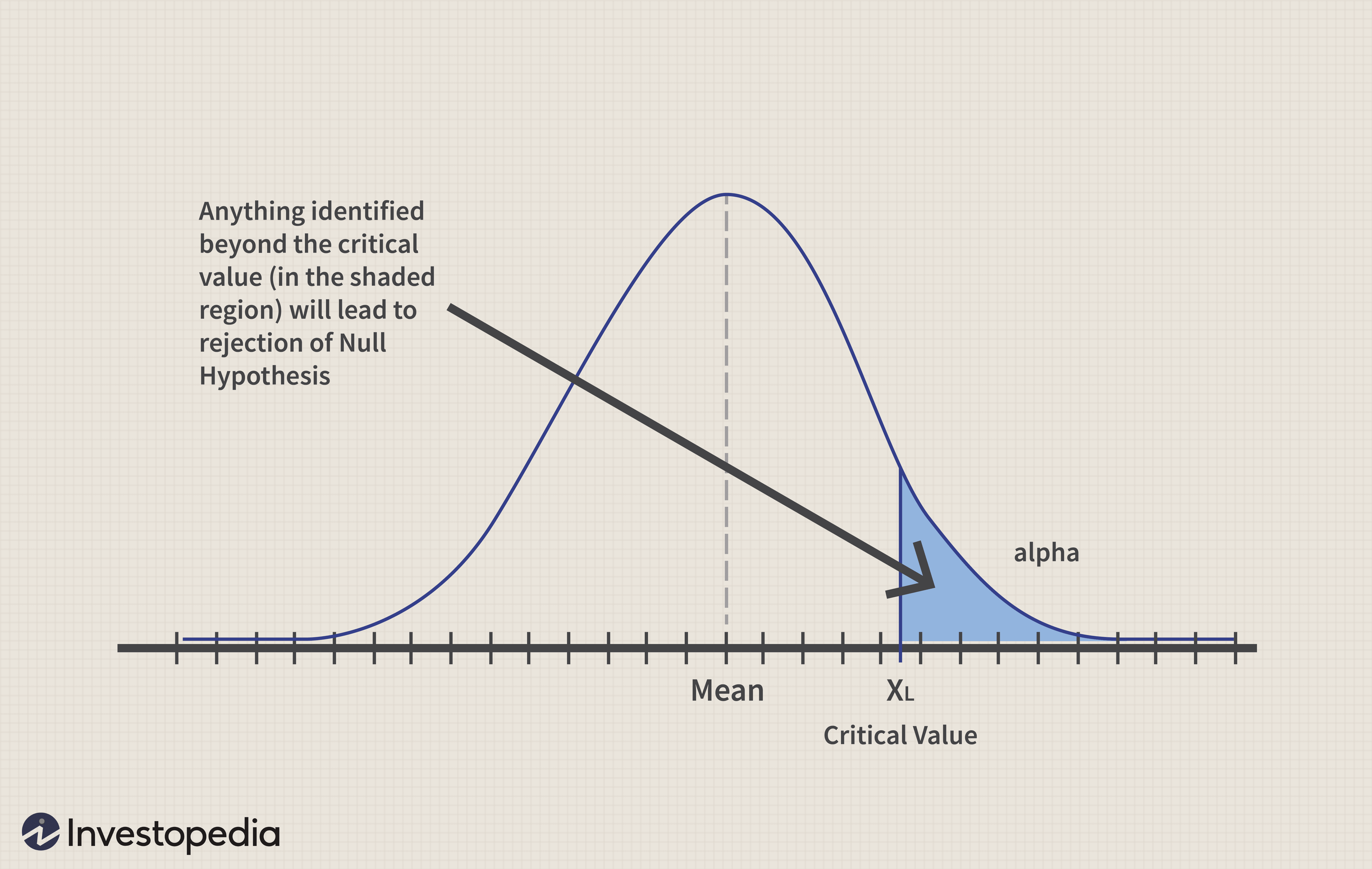
Alpha denota l'errore sul livello di significatività ed è determinato dal ricercatore. Per mantenere la significatività o il livello di confidenza standard del 5% per i calcoli di probabilità, questo viene mantenuto al 5%.
Secondo i parametri e le definizioni decisionali applicabili:
- “Questo criterio (alfa) è solitamente fissato a 0,05 (a =0,05), e confrontiamo il livello alfa con il p-value. Quando la probabilità di un errore di tipo I è inferiore al 5% (p <0,05), decidiamo di rifiutare l'ipotesi nulla; altrimenti, manteniamo l'ipotesi nulla.”
- Il termine tecnico utilizzato per questa probabilità è il valore p . È definita come “la probabilità di ottenere un risultato campionario, dato che il valore dichiarato nell'ipotesi nulla è vero. Il p-value per ottenere un risultato del campione viene confrontato con il livello di significatività."
- Un errore di tipo II, o errore beta, è definita come la probabilità di ritenere erroneamente l'ipotesi nulla, quando in realtà non è applicabile a tutta la popolazione.
Alcuni altri esempi dimostreranno questo e altri calcoli.
Esempio 1
Esiste uno schema di investimento a reddito mensile che promette rendimenti mensili variabili. Un investitore investirà in esso solo se gli viene assicurato un reddito mensile medio di $ 180. L'investitore ha un campione di rendimenti di 300 mesi che ha una media di $ 190 e una deviazione standard di $ 75. Dovrebbero investire in questo schema?
Impostiamo il problema. L'investitore investirà nello schema se è sicuro del rendimento medio desiderato di $ 180 dell'investitore.
h 0 :Ipotesi nulla:media =180
h 1 :Ipotesi alternativa:media> 180
Metodo 1: Approccio al valore critico
Identificare un valore critico X l per la media campionaria, che è abbastanza grande da rifiutare l'ipotesi nulla, ovvero rifiutare l'ipotesi nulla se la media campionaria>=valore critico X l
P (identifica un errore alfa di tipo I) =P (rifiuta H 0 dato che H 0 è vero),
Ciò si otterrebbe quando la media campionaria supera i limiti critici.
=P (dato che H 0 è vero) =alfa
Graficamente, appare come segue:
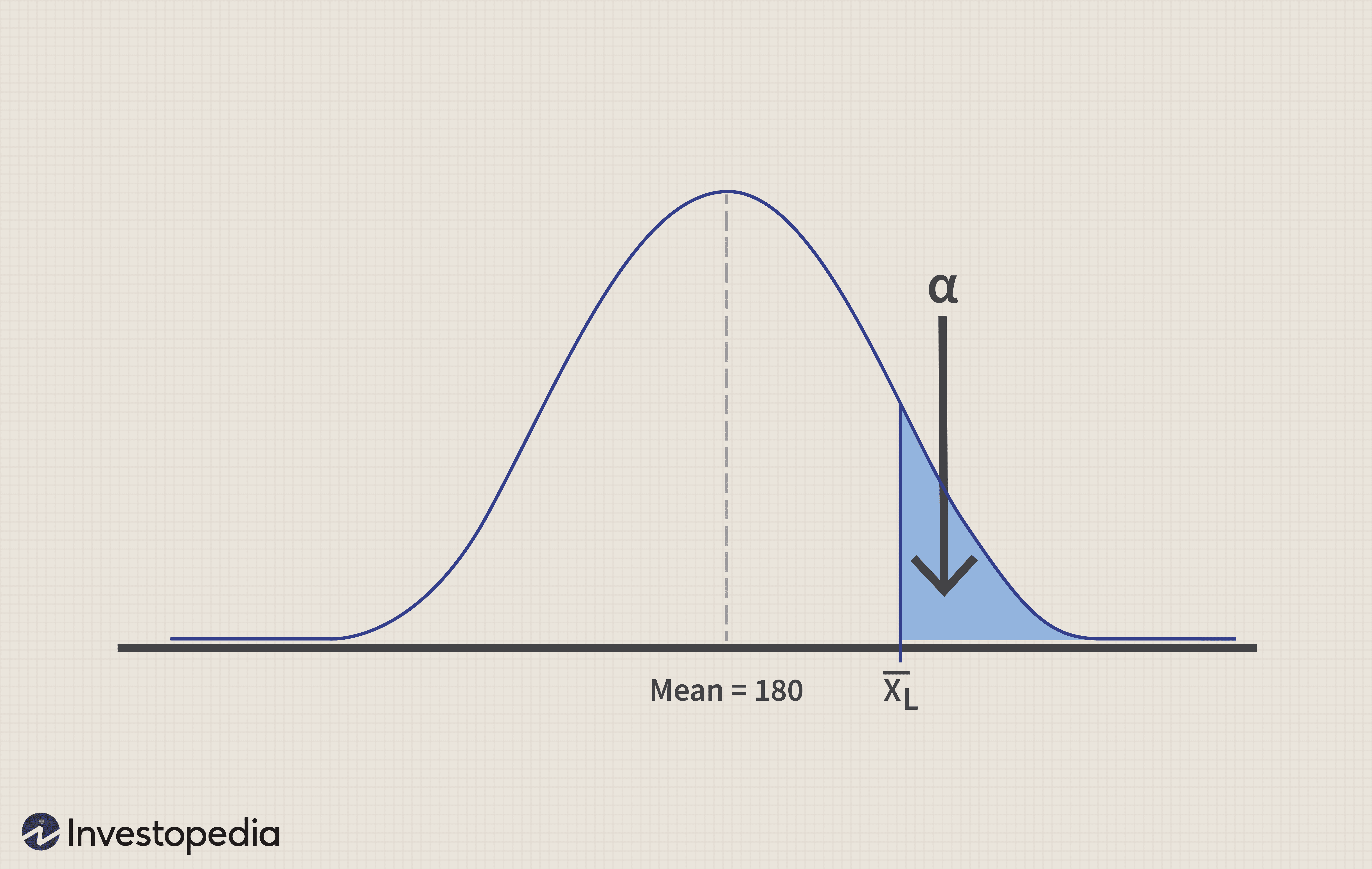
Prendendo alfa =0,05 (cioè livello di significatività del 5%), Z 0.05 =1.645 (dalla tabella Z o dalla tabella di distribuzione normale)
=> X l =180 +1.645*(75/quadrato(300)) =187.12
Poiché la media campionaria (190) è maggiore del valore critico (187.12), l'ipotesi nulla è respinta, e la conclusione è che il rendimento mensile medio è effettivamente maggiore di $ 180, quindi l'investitore può considerare di investire in questo schema.
Metodo 2: utilizzo di statistiche di test standardizzate
Si può anche usare il valore standardizzato z.
Statistica di prova, Z =(media del campione – media della popolazione) / (std-dev / sqrt (n. di campioni).
Quindi, la regione di rifiuto diventa la seguente:
Z=(190 – 180) / (75 / sqrt (300)) =2.309
La nostra regione di rifiuto al livello di significatività del 5% è Z> Z 0.05 =1,645.
Poiché Z=2.309 è maggiore di 1.645, l'ipotesi nulla può essere respinta con un'analoga conclusione di cui sopra.
Metodo 3: calcolo del valore P
Ci proponiamo di identificare P (media campionaria>=190, quando media =180).
=P (Z>=(190- 180) / (75 / sqrt (300))
=P (Z>=2,309) =0,0084 =0,84%
La seguente tabella per dedurre i calcoli del p-value conclude che vi sono prove confermate di rendimenti mensili medi superiori a 180:
valore p
Inferenza
meno dell'1%
Prove confermate supportando ipotesi alternative
tra 1% e 5%
Forte evidenza supportando ipotesi alternative
tra il 5% e il 10%
prove deboli supportando ipotesi alternative
maggiore del 10%
Nessuna prova supportando ipotesi alternative
Esempio 2
Un nuovo agente di cambio (XYZ) afferma che le sue commissioni di intermediazione sono inferiori a quelle del tuo attuale agente di cambio (ABC). I dati disponibili da una società di ricerca indipendente indicano che la media e lo std-dev di tutti i clienti dei broker ABC sono $ 18 e $ 6, rispettivamente.
Viene prelevato un campione di 100 clienti di ABC e calcolate le spese di intermediazione con le nuove tariffe del broker XYZ. Se la media del campione è $ 18,75 e std-dev è lo stesso ($ 6), si può fare qualche deduzione sulla differenza nella fattura di intermediazione media tra il broker ABC e XYZ?
h 0 :Ipotesi nulla:media =18
h 1 :Ipotesi alternativa:media <> 18 (Questo è ciò che vogliamo dimostrare.)
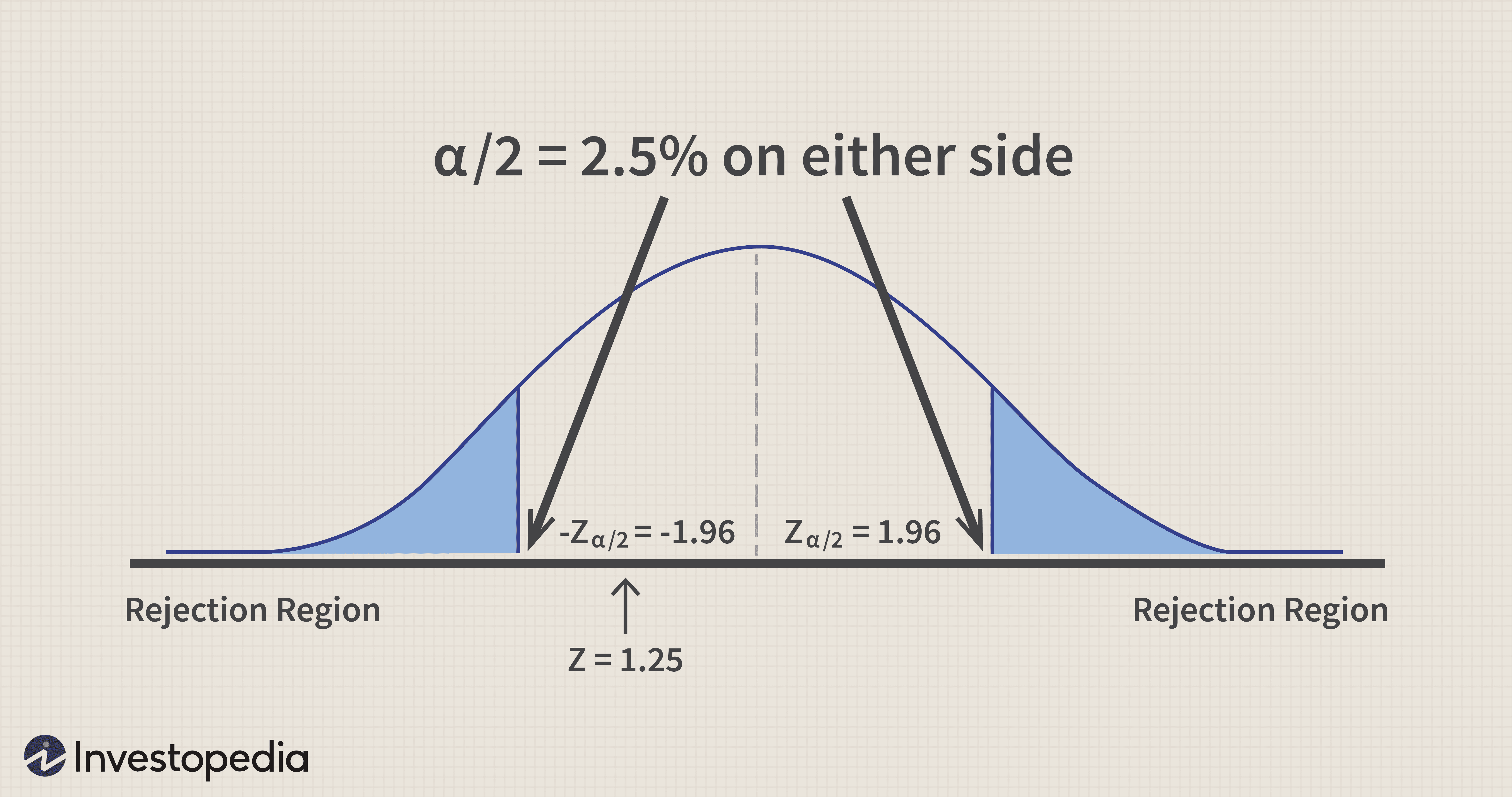
Regione di rifiuto:Z <=- Z 2,5 e Z>=Z 2,5 (assumendo un livello di significatività del 5%, dividere 2,5 ciascuno su entrambi i lati).
Z =(campione media – media) / (std-dev / sqrt (n. di campioni))
=(18,75 – 18) / (6/(quadrato(100)) =1,25
Questo valore Z calcolato rientra tra i due limiti definiti da:
- Z 2,5 =-1,96 e Z 2,5 =1,96.
Ciò conclude che non ci sono prove sufficienti per dedurre che ci sia una differenza tra le tariffe del tuo broker esistente e il nuovo broker.
In alternativa, Il valore p =P(Z<-1,25)+P(Z>1,25)
=2 * 0,1056 =0,2112 =21,12% che è maggiore di 0,05 o 5%, portando alla stessa conclusione.
Graficamente, è rappresentato da quanto segue:
Punti critici per il metodo di test ipotetico:
- Un metodo statistico basato su ipotesi
- Soggetto a errori come dettagliato in termini di errori alfa e beta
- L'interpretazione del p-value può essere ambigua, portando a risultati confusi
La linea di fondo
Il test di ipotesi consente a un modello matematico di convalidare un'affermazione o un'idea con un certo livello di confidenza. Però, come la maggior parte degli strumenti e dei modelli statistici, è vincolato da alcune limitazioni. L'uso di questo modello per prendere decisioni finanziarie dovrebbe essere considerato con occhio critico, tenendo a mente tutte le dipendenze. Vale la pena esplorare anche metodi alternativi come l'inferenza bayesiana per un'analisi simile.
Trading di futures
- Futures sull'indice azionario CME Micro E-mini visti come un'offerta favorevole al dettaglio; Aggiornamento Futures Bitcoin
- Azionista attivista
- Oscillazioni di mercato:perché alcuni trader amano la volatilità del mercato?
- Introduzione all'interesse aperto nel mercato dei futures
- Tic Tac
- Cinque vantaggi dei future rispetto alle opzioni
-
 Non lasciarti ingannare:il Petro del Venezuela non è davvero una criptovaluta
Non lasciarti ingannare:il Petro del Venezuela non è davvero una criptovaluta Il Venezuela sta soffrendo una delle peggiori crisi economiche dei tempi moderni. Il governo assediato del presidente Nicolás Maduro sta supervisionando la scarsità di cibo e medicine, laumento dei ta...
-
 Cos'è l'effetto gennaio?
Cos'è l'effetto gennaio? Leffetto gennaio è noto per essere un aumento stagionale dei prezzi delle azioni per tutto il mese di gennaio. Laumento della domanda di scorte è spesso preceduto da una diminuzione del prezzo durante...
-
 L'autorità keniota mette in guardia le persone dall'investire in una società commerciale di Bitcoin che offre guadagni irrealistici
L'autorità keniota mette in guardia le persone dall'investire in una società commerciale di Bitcoin che offre guadagni irrealistici Lavvertimento arriva dopo che la CMA ha preso atto dellofferta di FxbitInvest che attirava il pubblico keniota a investire i propri fondi promettendo un enorme ritorno del 400% in 6 ore. (Immagine rap...
-
 Affitta il tuo diploma a Natural Light per $ 100
Affitta il tuo diploma a Natural Light per $ 100 Hai presente quel pezzo di carta incorniciato sul muro del tuo ufficio che è costato molto da ottenere? Ora, quel diploma universitario può farti ottenere più di unofferta di lavoro. Luce naturale, ...




