Definizione del teorema di Bayes
Che cos'è il teorema di Bayes?
Teorema di Bayes, prende il nome dal matematico britannico del XVIII secolo Thomas Bayes, è una formula matematica per determinare la probabilità condizionata. La probabilità condizionata è la probabilità che si verifichi un risultato, sulla base di un esito precedente verificatosi. Il teorema di Bayes fornisce un modo per rivedere le previsioni o le teorie esistenti (aggiornare le probabilità) date prove nuove o aggiuntive. In finanza, Il teorema di Bayes può essere utilizzato per valutare il rischio di prestare denaro a potenziali mutuatari.
Il teorema di Bayes è anche chiamato Regola di Bayes o Legge di Bayes ed è il fondamento del campo della statistica bayesiana.
Punti chiave
- Il teorema di Bayes consente di aggiornare le probabilità previste di un evento incorporando nuove informazioni.
- Il teorema di Bayes prende il nome dal matematico del XVIII secolo Thomas Bayes.
- È spesso impiegato in finanza per aggiornare la valutazione del rischio.
Comprensione del teorema di Bayes
Le applicazioni del teorema sono diffuse e non limitate all'ambito finanziario. Come esempio, Il teorema di Bayes può essere utilizzato per determinare l'accuratezza dei risultati dei test medici prendendo in considerazione la probabilità che una data persona abbia una malattia e l'accuratezza generale del test. Il teorema di Bayes si basa sull'incorporazione di distribuzioni di probabilità precedenti per generare probabilità a posteriori. Probabilità a priori, nell'inferenza statistica bayesiana, è la probabilità di un evento prima che vengano raccolti nuovi dati. Questa è la migliore valutazione razionale della probabilità di un risultato basata sulle conoscenze attuali prima che venga eseguito un esperimento. La probabilità a posteriori è la probabilità rivista di un evento che si verifica dopo aver preso in considerazione nuove informazioni. La probabilità a posteriori viene calcolata aggiornando la probabilità a priori utilizzando il teorema di Bayes. In termini statistici, la probabilità a posteriori è la probabilità che l'evento A si verifichi dato che l'evento B si è verificato.
Il teorema di Bayes fornisce quindi la probabilità di un evento sulla base di nuove informazioni che è, o può essere correlato, a quell'evento. La formula può essere utilizzata anche per vedere come la probabilità che si verifichi un evento sia influenzata da ipotetiche nuove informazioni, supponendo che le nuove informazioni si rivelino vere. Ad esempio, diciamo che una singola carta viene estratta da un mazzo completo di 52 carte. La probabilità che la carta sia un re è quattro diviso 52, che equivale a 1/13 o circa il 7,69%. Ricorda che ci sono quattro re nel mazzo. Ora, supponiamo che venga rivelato che la carta selezionata è una figura. La probabilità che la carta selezionata sia un re, dato che è una figura, è quattro diviso 12, o circa il 33,3%, dato che ci sono 12 figure in un mazzo.
Formula per il teorema di Bayes
Esempi del teorema di Bayes
Di seguito sono riportati due esempi del teorema di Bayes in cui il primo esempio mostra come la formula può essere derivata in un esempio di investimento azionario utilizzando Amazon.com Inc. (AMZN). Il secondo esempio applica il teorema di Bayes ai test sui farmaci.
Derivazione della formula del teorema di Bayes
Il teorema di Bayes segue semplicemente dagli assiomi della probabilità condizionata. La probabilità condizionata è la probabilità di un evento dato che si è verificato un altro evento. Per esempio, una semplice domanda sulla probabilità può chiedere:"Qual è la probabilità che il prezzo delle azioni di Amazon.com scenda?" La probabilità condizionata porta questa domanda un ulteriore passo avanti chiedendo:"Qual è la probabilità che il prezzo delle azioni AMZN scenda? dato che l'indice Dow Jones Industrial Average (DJIA) è sceso prima?"
La probabilità condizionata di A dato che B si è verificato può essere espressa come:
Se A è:"Il prezzo AMZN scende", allora P(AMZN) è la probabilità che AMZN diminuisca; e B è:"DJIA è già giù, " e P(DJIA) è la probabilità che il DJIA sia diminuito; quindi l'espressione di probabilità condizionale si legge come "la probabilità che AMZN diminuisca in caso di un declino DJIA è uguale alla probabilità che il prezzo AMZN diminuisca e DJIA diminuisca rispetto alla probabilità di una diminuzione l'indice DJIA.
P(AMZN|DJIA) =P(AMZN e DJIA) / P(DJIA)
P(AMZN e DJIA) è la probabilità di entrambi A e B che si verificano. Questa è anche la stessa della probabilità che si verifichi A moltiplicata per la probabilità che si verifichi B dato che si verifica A, espresso come P(AMZN) x P(DJIA|AMZN). Il fatto che queste due espressioni siano uguali porta al teorema di Bayes, che si scrive come:
Se, P(AMZN e DJIA) =P(AMZN) x P(DJIA|AMZN) =P(DJIA) x P(AMZN|DJIA)
poi, P(AMZN|DJIA) =[P(AMZN) x P(DJIA|AMZN)] / P(DJIA).
Dove P(AMZN) e P(DJIA) sono le probabilità di caduta di Amazon e Dow Jones, senza riguardo gli uni agli altri.
La formula spiega la relazione tra la probabilità dell'ipotesi prima di vedere l'evidenza che P(AMZN), e la probabilità dell'ipotesi dopo aver ottenuto l'evidenza P(AMZN|DJIA), data un'ipotesi per Amazon data evidenza nel Dow.
Esempio numerico del teorema di Bayes
Come esempio numerico, immagina che ci sia un test antidroga accurato al 98%, il che significa che il 98% delle volte mostra un vero risultato positivo per qualcuno che usa il farmaco e il 98% delle volte mostra un vero risultato negativo per i non utilizzatori del farmaco. Prossimo, supponiamo che lo 0,5% delle persone usi il farmaco. Se una persona selezionata a caso risulta positiva al farmaco, si può fare il seguente calcolo per vedere se la probabilità che la persona sia effettivamente un utilizzatore della droga.
(0,98 x 0,005) / [(0,98 x 0,005) + ((1 - 0,98) x (1 - 0,005))] =0,0049 / (0,0049 + 0,0199) =19,76%
Il teorema di Bayes mostra che anche se una persona risultasse positiva in questo scenario, in realtà è molto più probabile che la persona non sia un utilizzatore del farmaco.
finanza
- Definizione di assunzione del debito
- Definizione di co-candidato
- Definizione di controllo di routine
- Definizione della media geometrica
- Definizione di valutazione
- Definizione e spiegazione del collaterale
- Una definizione di tempi di interesse guadagnato
- Liquidità - Definizione e indici
- Definizione e spiegazione dell'esborso
- Fiduciario - Definizione e responsabilità
-
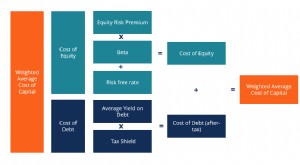 Definizione di WACC
Definizione di WACC Il costo medio ponderato del capitale (WACC) di unimpresa rappresenta il suo costo misto del capitale Il costo del capitale Il costo del capitale è il tasso di rendimento minimo che unazienda deve gua...
-
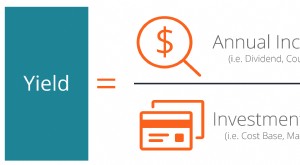 Che cos'è il rendimento (definizione)?
Che cos'è il rendimento (definizione)? Il rendimento è definito come un ritorno sullinvestimento basato sul solo reddito (esclude le plusvalenze Capital Gain YieldCapital gains yield (CGY) è lapprezzamento del prezzo di un investimento o d...