Definizione della media geometrica
Qual è la media geometrica?
La media geometrica è la media di un insieme di prodotti, il cui calcolo è comunemente utilizzato per determinare i risultati di performance di un investimento o di un portafoglio. È tecnicamente definito come "the nth prodotto radice di n numeri." La media geometrica deve essere utilizzata quando si lavora con percentuali, che derivano da valori, mentre la media aritmetica standard lavora con i valori stessi.
La media geometrica è uno strumento importante per calcolare la performance del portafoglio per molte ragioni, ma uno dei più significativi è che tiene conto degli effetti della capitalizzazione.
Punti chiave
- La media geometrica è il tasso di rendimento medio di un insieme di valori calcolato utilizzando i prodotti dei termini.
- La media geometrica è più appropriata per le serie che mostrano una correlazione seriale, questo è particolarmente vero per i portafogli di investimento.
- La maggior parte dei rendimenti finanziari sono correlati, compresi i rendimenti delle obbligazioni, rendimenti azionari, e premi per il rischio di mercato.
- Per i numeri volatili, la media geometrica fornisce una misurazione molto più accurata del rendimento reale tenendo conto della capitalizzazione anno su anno che livella la media.
La formula per la media geometrica
Capire la media geometrica
La media geometrica, a volte indicato come tasso di crescita annuale composto o tasso di rendimento ponderato nel tempo, è il tasso di rendimento medio di un insieme di valori calcolato utilizzando i prodotti dei termini. Che cosa significa? La media geometrica prende diversi valori e li moltiplica tra loro e li imposta a 1/n ns potenza.
Per esempio, il calcolo della media geometrica può essere facilmente compreso con semplici numeri, come 2 e 8. Se moltiplichi 2 e 8, quindi prendi la radice quadrata (la ½ potenza poiché ci sono solo 2 numeri), la risposta è 4. Tuttavia, quando ci sono molti numeri, è più difficile da calcolare a meno che non venga utilizzata una calcolatrice o un programma per computer.
Più lungo è l'orizzonte temporale, il composto più critico diventa, e più appropriato l'uso della media geometrica.
Il vantaggio principale dell'utilizzo della media geometrica è che non è necessario conoscere gli importi effettivi investiti; il calcolo si concentra interamente sulle cifre del rendimento stesso e presenta un confronto "dalle mele alle mele" quando si esaminano due opzioni di investimento in più di un periodo di tempo. Le medie geometriche saranno sempre leggermente più piccole della media aritmetica, che è una media semplice.
Come calcolare la media geometrica
Per calcolare l'interesse composto utilizzando la media geometrica del rendimento di un investimento, un investitore deve prima calcolare l'interesse nel primo anno, che è $ 10, 000 moltiplicato per 10%, o $ 1, 000. Nel secondo anno, il nuovo importo del capitale è di $ 11, 000, e il 10% di $ 11, 000 è $ 1, 100. Il nuovo importo principale è ora di $ 11, 000 più $ 1, 100, o $12, 100.
Nel terzo anno, il nuovo importo del capitale è di $ 12, 100, e il 10% di $ 12, 100 è $ 1, 210. Alla fine dei 25 anni, i $ 10, 000 si trasforma in $ 108, 347.06, che è $ 98, 347,05 in più rispetto all'investimento originario. La scorciatoia è moltiplicare il capitale corrente per uno più il tasso di interesse, e quindi aumentare il fattore al numero di anni composti. Il calcolo è di $ 10, 000 × (1+0,1) 25 =$ 108, 347.06.
1:23Media geometrica
Esempio di media geometrica
Se hai $ 10, 000 e ricevi un interesse del 10% su quei $ 10, 000 ogni anno per 25 anni, l'importo degli interessi è $ 1, 000 ogni anno per 25 anni, o $ 25, 000. Tuttavia, questo non tiene conto dell'interesse. Questo è, il calcolo presuppone che tu riceva solo gli interessi sui $ 10 originali, 000, non il $ 1, 000 aggiunti ad esso ogni anno. Se l'investitore riceve un interesse sugli interessi, si parla di interesse composto, che viene calcolato utilizzando la media geometrica.
L'utilizzo della media geometrica consente agli analisti di calcolare il rendimento di un investimento che riceve interessi sugli interessi. Questo è uno dei motivi per cui i gestori di portafoglio consigliano ai clienti di reinvestire dividendi e utili.
La media geometrica viene utilizzata anche per le formule del flusso di cassa del valore attuale e del valore futuro. Il rendimento medio geometrico viene utilizzato specificamente per gli investimenti che offrono un rendimento composto. Tornando all'esempio sopra, invece di guadagnare solo $25, 000 su un investimento a semplice interesse, l'investitore guadagna $ 108, 347.06 su un investimento a capitalizzazione.
L'interesse semplice o rendimento è rappresentato dalla media aritmetica, mentre l'interesse composto o il rendimento è rappresentato dalla media geometrica.
finanza
- Definizione di valutazione
- Definizione del teorema di Bayes
- Abbattere la media geometrica negli investimenti
- Definizione e spiegazione del collaterale
- Una definizione di tempi di interesse guadagnato
- Liquidità - Definizione e indici
- Definizione e spiegazione dell'esborso
- Definizione di fallimento:cosa significa esattamente?
- Reddito fisso:media geometrica vs media aritmetica
- Significato aritmetico
-
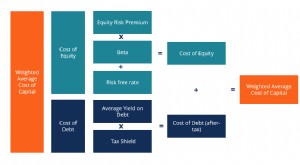 Definizione di WACC
Definizione di WACC Il costo medio ponderato del capitale (WACC) di unimpresa rappresenta il suo costo misto del capitale Il costo del capitale Il costo del capitale è il tasso di rendimento minimo che unazienda deve gua...
-
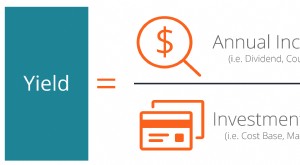 Che cos'è il rendimento (definizione)?
Che cos'è il rendimento (definizione)? Il rendimento è definito come un ritorno sullinvestimento basato sul solo reddito (esclude le plusvalenze Capital Gain YieldCapital gains yield (CGY) è lapprezzamento del prezzo di un investimento o d...